问题
问答题
设抛物线y=ax2+bx+c满足:①通过两点(0,0)和(1,2);②与抛物线y=-x2+2x所围图形的面积最小.试求:a,b,c的值.
答案
参考答案:
解析: 由①知,(0,0)在抛物线上,故c=0.
又a+b=2,所以抛物线的方程为y=ax2+(2-a)x.
由②,先求两条抛物线的交点坐标:
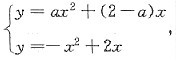
解得
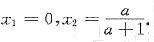 故所围面积为
故所围面积为

即所求抛物线为:y=-3x2+5x.
设抛物线y=ax2+bx+c满足:①通过两点(0,0)和(1,2);②与抛物线y=-x2+2x所围图形的面积最小.试求:a,b,c的值.
参考答案:
解析: 由①知,(0,0)在抛物线上,故c=0.
又a+b=2,所以抛物线的方程为y=ax2+(2-a)x.
由②,先求两条抛物线的交点坐标:
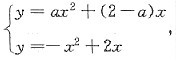
解得
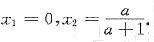 故所围面积为
故所围面积为

即所求抛物线为:y=-3x2+5x.