问题
单项选择题
设三元方程为x2y-2zlny+exz=1,根据隐函数存在定理,存在点(0,1,2)的一个邻域,在此邻域内,该方程______
A.只能确定一个具有连续偏导数的隐函数:z=z(x,y).
B.可以确定两个具有连续偏导数的隐函数:y=y(x,z)和z=z(x,y).
C.可以确定两个具有连续偏导数的隐函数:z=x(y,z)和z=z(x,y).
D.可以确定两个具有连续偏导数的隐函数:z=x(y,z)和y=y(x,z).
答案
参考答案:D
解析: 令F(x,y,z)=x2y-2zlny十exz-1,则F(0,1,2)=0,且
F’x(0,1,2)=(2xy+zexz)|(0,1,2)=2≠0,
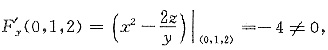
F’x(0,1,2)=(-2lny)|(0,1,2)=0.
所以,在点(0,1,2)的一个邻域内,该方程可以确定两个具有连续偏导数的隐函数:x=x(y,z)和y=y(x,z),
而不能确定z=z(x,y),故选D.
