问题
问答题
有非零解，且
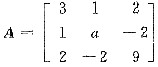是正定矩阵，求a；当XTX=2时，求XTAX的最大值．
答案
参考答案：由于方程组有非零解，有
[*]
由于A是正定矩阵，必有a＞0，可排除a=0或-1．
当a=3时
[*]
=(λ-4)(λ-1)(λ-10)．
A的特征值全大于0，知A正定，即a=3适合于要求A是实对称矩阵，故存在正交矩阵P，经X=PY化二次型XTAX为标准形．由于
YTY=YTPTPY=(PY)T(PY)=XTX=2，
可见[*]
因此 XTX=2时，XTAX的最大值是20．
解析：
[分析]： 考查齐次方程组有非零解的条件及矩阵正定的条件．