问题
问答题
设有方程
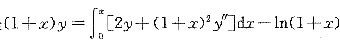 ,其中x≥0,且有y’(0)=0,求方程所确定的函数y.
,其中x≥0,且有y’(0)=0,求方程所确定的函数y.
答案
参考答案:令1+x=et,即t=ln(1+x),则方程
[*]
可化为 y"-2y’+y=e-t,
其对应的齐次方程的通解为
y1=(C1+C2t)et,
非齐次方程的特解为[*]
故原方程的通解为
[*]
由初始条件y(0)=y’(0)=0,可求得
[*]
于是原方程所确定的函数为
[*]
解析:
[分析]: 若在方程两边对x求导,化简可得[*],且y(0)=y’(0)=0.
这是形如
(ax+b)ny(n)+a1(a+b)n-1y(n-1)+…+an-1(ax+b)y’+any=f(x)
的欧拉方程,只要令ax+b=et,就可把方程化为常系数线性方程.
