问题
多项选择题
设f(x)为连续、单减函数,x∈(-∞,+∞),且
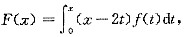
试证F(x)为单增函数,x∈(-∞,+∞).
答案
参考答案:由题设知F(x)连续且可导,得
[*]
由f(x)单减,故当0<t<x,有f(t)-f(x)≥0,再由定积分性质,知F’(x)≥0;当x<t<0,有f(t)-f(x)≤0,于是
[*]
总之,F’(x)≥0,x∈(-∞,+∞),从而F(x)单增,x∈(-∞,+∞).
解析:
[分析]: 欲证F(x)单增,即要证F’(x)≥0.
