问题
问答题
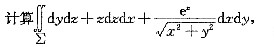
其中∑是锥面
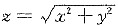 被平面z=1与z=2所截得的部分的下侧.
被平面z=1与z=2所截得的部分的下侧.
答案
参考答案:解法一 逐块计算.
[*]
其中∑=∑3+∑4,∑3表示前块(即∑3的法向量与y轴正向成锐角),∑4表示后块(即∑4的法向量与x轴正向成钝角),它们有共同的投影域Dyz.
[*]
其中∑=∑3+∑4,∑3表示右块(即∑3的法向量与y轴正向成锐角),∑4表示左块(即∑4的法向量与y轴正向成钝角),Dzx为其投影域.
[*]
其中Dxy为∑在xOy平面的投影域,因∑取下侧,故∑在xOy平面上的投影为负.
解法二 利用高斯公式.
添补辅助面两块:∑上与∑下,使∑+∑上+∑下成为封闭曲面,以便用高斯公式进行计算.
[*]
[*]
因此,
[*]
=2πe(1-e).
解析:
[分析]: 可以逐块进行计算,也可以利用高斯公式计算(此时要添补两块辅助面,使之成为封闭曲面).
