设总体X的概率密度为
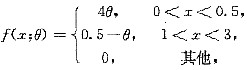
其中θ(0<θ<0.5)是未知参数,从总体X中抽取样本值如下:
0.3,1.8,0.2,0.1,0.4,2.1,1.9,2.6,0.4,0.2,
求:(Ⅰ)θ的矩估计值;
(Ⅱ)θ的最大似然估计值.
参考答案:(Ⅰ)由于
[*]
样本平均值为[*]=1,令μ=[*],即
2-3.50=1.
解得[*],因此θ的矩估计值为[*]=0.29.
(Ⅱ)对于给定的样本值,似然函数为
[*]
取对数,得
lnL(θ)=6(ln4+lnθ)+4ln(0.5-θ)
=6(ln4+lnθ)+4[ln(1-2θ)-ln2],
将lnL(θ)对θ求导数并令其等于零,得
[*]
解得θ=0.3,即θ的最大似然估计值为
[*]=0.3.
解析:
[分析]: 算出E(X)及样本值的平均值[*],即可得到θ的矩估计值。根据样本值正确地写出似然函数L(θ)的表达式,是求θ的最大似然估计值的关键.对于样本值x1,x2…,xn,似然函数[*].当x1=0.3时,(0.3;θ)=4θ;当x2=1.8时,f(1.8;θ)=0.5-θ;…;当x10=0.2时,f(0.2;θ)=4θ.对于给定的样本值,在(0,0.5)内的有6个数,在(1,3)内的有4个数,因此似然函数L(θ)=(4θ)6(0.5-θ)4.
