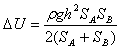如图所示,A、B容器中各有一个可自由移动的轻活塞,活塞下是水,上为空气,大气压恒定,A、B底部由带有阀门K的管道相连,整个装置与外界绝热,原先A中水面比B中高,打开阀门,使A中的水逐渐向B中流,最后达到平衡,则在这个过程中,大气压力对水做功是多少?水的内能增加了多少?(已知水的密度为ρ,活塞面积分别为SA、SB,原来A、B中高度差为h)

解:打开阀门K后,根据连通器原理,最后A、B两管中的水面将相平,即A中的水面下降,B中的水面上升,设A中水面下降hA,B管水面上升的距离为hB,由于水的总体积保持不变,故:SAhA=SBhB
A管中的水受到向下的大气压力,与水面下降的方向相同,所以大气压力对水做正功,设大气压强为P0,对水做的功为W1,则:W1=F1hA=P0SAhA
B管中的水也受到向下的大气压力,与水面上升的方向相反,所以大气压力对水做负功,用W2表示大气压力做的功,有:W2=-F2hB= -P0SBhB
大气压力对水做的总功为:W=W1+W2=P0SAhA-P0SBhB
又SAhA=SBhB
所以W=0,即大气压力对水不做功
阀门打开后,水从高处流向低处,在这个过程中水的重力做正功,所以水的内能增加量等于水的重力势能的减小量
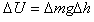 ,其中
,其中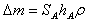 ,
,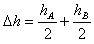
又SAhA=SBhB,hA+hB=h
由以上各式解得