已知某工程双代号网络计划如图7-3所示,图中箭线下方括号外数字为工作的正常持续时间,括号内数字为最短持续时间:箭线上方括号内数字为优选系数,该系数综合考虑质量、安全和费用增加情况而确定。选择关键工作压缩其持续时间时,应选择优选系数最小的关键工作。若需要同时压缩多个关键工作的持续时间时,则它们的优选系数之和(组合优选系数)最小者应作为优先压缩对象。现假设要求工期为15天。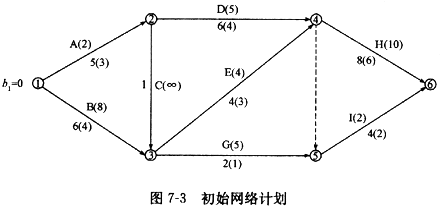
【问题】1. 试对其进行工期优化。
参考答案:
该网络计划的工期优化可按以下步骤进行:
(1)根据各项工作的正常持续时间,用标号法确定网络计划的计算工期和关键线路,如图7-4所示。此时关键线路为①—②—④—⑥。
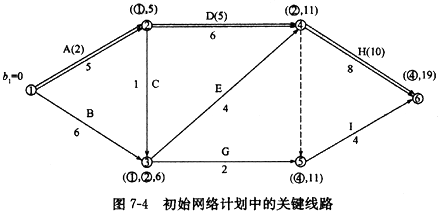
(2)计算应缩短的时间:
△T=Tc-Tr=19-15=4(天)
(3)由于此时关键工作为工作A、工作D和工作H,而其中工作A的优选系数最小,故应将工作A作为优先压缩对象。
(4)将关键工作A的持续时间压缩至最短持续时间3,利用标号法确定新的计算工期和关键线路,如图7-5所示。此时,关键工作A被压缩成非关键工作,故将其持续时间3延长为4,使之成为关键工作。工作A恢复为关键工作之后,网络计划中出现两条关键线路,即:①—②—④—⑥和①—③—④—⑥,如图7-6所示。

(5)由于此时计算工期为18,仍大于要求工期,故需继续压缩.需要缩短的时间:△T1=18-15=3 (天).在图7-6所示网络计划中,有以下五个压缩方案:
①同时压缩工作A和工作B,组合优选系数为:2+8=10;
②同时压缩工作A和工作E,组合优选系数为:2+4=6;
③同时压缩工作B和工作D,组合优选系数为:8+5=13;
④同时压缩工作D和工作E,组合优选系数为:5+4=9;
⑤压缩工作H,优选系数为10。
在上述压缩方案中,由于工作A和工作E的组合优选系数最小,故应选择同时压缩工作A和工作E的方案。将这两项工作的持续时间各压缩1天(压缩至量短),再用标号法确定计算工期和关键线路,如图7-7所示.此时,关键线路仍为两条,即,①—②—④一⑥和①—③—④—⑥。
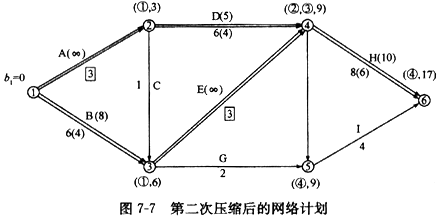
在图7-7中,关键工作A和E的持续时间已达最短,不能再压缩,它们的优选系数变为无穷大。
(6)由于此时计算工期为17,仍大于要求工期,故需继续压缩。需要缩短的时间:△T2=17-15=2(天)。在图7-7所示网络计划中,由于关键工作A和E已不能再压缩,故此时只有两个压缩方案;
①同时压缩工作B和工作D,组合优选系数为:8+5=13;
②压缩工作H,优选系数为10。
在上述压缩方案中,由于工作H的优选系数最小,故应选择压缩工作H的方案。将工作H的持续时间缩短2,再用标号法确定计算工期和关键线路,如图7-8所示。此时,计算工期为15,等于要求工期,故图7-8所示网络计划即为优化方案。

