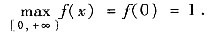问题
问答题
设
(Ⅰ) 求证：f(x)在[0，+∞)上连续；
(Ⅱ) 求f(x)在[0，+∞)的单调性区间；
(Ⅲ) 求f(x)在[0，+∞)的最大值与最小值．
答案
参考答案：(Ⅰ) 当x＞0时f(x)与初等函数
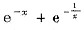相同，故连续．又
即f(x)在x=0处右连续，因此f(x)在[0，+∞)上连续．
(Ⅱ) 考察(0，+∞)上f’(x)的符号．先求
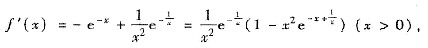
并考察
，由
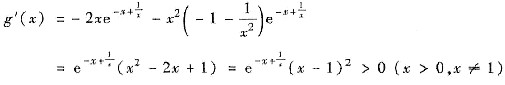
g(x)在(0，+∞)单调上升
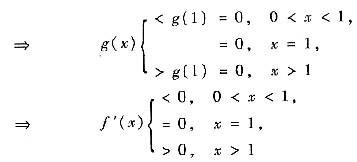
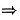f(x)在[0，1]单调下降，在[1，+∞)单调上升．
(Ⅲ) 由上述单调性分析知，
又
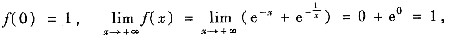
因此
