问题
问答题
已知A是3阶矩阵,αi(i=1,2,3)是3维非零列向量,若Aαi=iαi(i=1,2,3),令
α=α1+α2+α3.
(Ⅰ) 证明:α,Aα,A2α线性无关;
(Ⅱ) 设P=(α,Aα,A2α),求P-1AP.
答案
参考答案:(Ⅰ) 由Aα1=α1,Aα2=2α2,Aα3=3α3,且α1,α2,α3非零可知,α1,α2,α3是A的不同特征值的特征向量,故α1,α2,α3线性无关.
又 Aα=α1+2α2+3α3,A2α=α1+4α2+9α3,若k1α+k2Aα+k3A2α=0,即
k1(α1+α2+α3)+k2(α1+2α2+3α3)+k3(α1+4α2+9α3)=0,
则 (k1+k2+k3)α1+(k1+2k2+4k3)α2+(k1+3k2+9k3)α3=0.
由α1,α2,α3线性无关,得齐次线性方程组
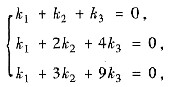
因为系数行列式为范德蒙行列式且其值不为0,所以必有k1=k2=k3=0,即α,Aα,A2α线性无关.
(Ⅱ) 因为A3α=α1+8α2+27α3=6α-11Aα+6A2α,所以
AP=A(α,Aα,A2α)=(Aα,A2α,6α-11Aα+6A2α)
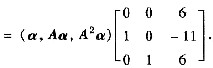
故