问题
问答题
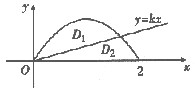
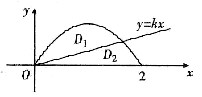
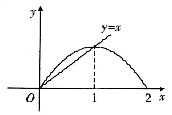
设D是曲线y=2x-x2与x轴围成的平面图形,直线y=kx把D分成为D1和D2两部分(如图),若D1的面积S1与D2的面积S2之比S1:S2=1:7.求平面图形D1的周长以及D1绕y轴旋转一周所得旋转体的体积.
答案
参考答案:由方程组
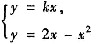 可解得直线y=kx与曲线y=2x-x2有两个交点(0,0)和(2-k,k(2-k)),其中0<k<2.于是
可解得直线y=kx与曲线y=2x-x2有两个交点(0,0)和(2-k,k(2-k)),其中0<k<2.于是
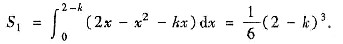
又
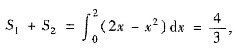
由题设 S1:S2=1:7,知
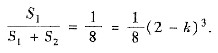
于是 k=1.
注意这时D1的边界由y=x上0≤x≤1的线段与曲线y=2x-x2上0≤x≤1的弧构成,从而D1的周长

于是D1绕y轴旋转一周所得旋转体的体积
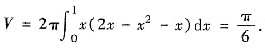
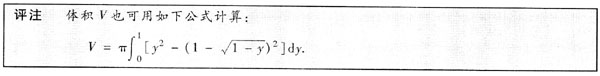

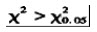 得到结果,正确的结论是()
得到结果,正确的结论是()