问题
问答题
设D=(x,y)|x2+y2≤1,
(Ⅰ) 将二重积分
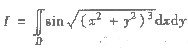 化为定积分;
化为定积分;
(Ⅱ) 证明不等式
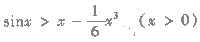 ;
;
(Ⅲ) 证明不等式
 .
.
答案
参考答案:(Ⅰ) 作极坐标变换化二重积分为定积分.
令x=rcosθ,y=rsinθ,则D:0≤0≤2π,0≤r≤1.于是
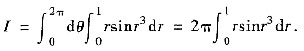
(Ⅱ) 利用单调性证明不等式.
令
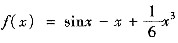 ,则f(x)在[0,+∞)内有二阶连续导数,且
,则f(x)在[0,+∞)内有二阶连续导数,且
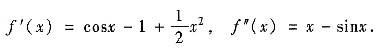
因sinx<x(x>0)
 f"(x)>0(x>0)
f"(x)>0(x>0)
 f’(x)在[0,+∞)单调上升,f’(x)>f’(0)=0(x>0)
f’(x)在[0,+∞)单调上升,f’(x)>f’(0)=0(x>0)
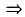 f(x)在[0,+∞)单调上升,f(x)>f(0)=0(x>0),即
f(x)在[0,+∞)单调上升,f(x)>f(0)=0(x>0),即
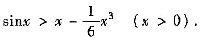
(Ⅲ) 由题(Ⅰ),估计
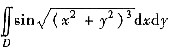 转化为估计定积分
转化为估计定积分
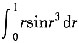 ,再利用sinx的不等式(题(Ⅱ)的不等式及sinx<x(x>0))来估计这个定积分.
,再利用sinx的不等式(题(Ⅱ)的不等式及sinx<x(x>0))来估计这个定积分.
由
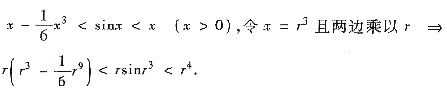 上 式两边在[0,1]上积分得
上 式两边在[0,1]上积分得
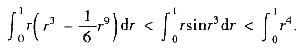
又
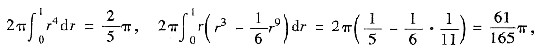
因此