问题
问答题
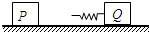
如图所示,位于光滑水平桌面上的小滑块P和Q都可视作质点,质量均为m,Q与轻质弹簧相连.设Q静止,P以某一初速度v0向Q运动并与弹簧发生碰撞,在压缩弹簧的整个碰撞过程中,求:
(1)当弹簧压缩最短时Q的速度为多大?
(2)弹簧具有的最大弹性势能等于多少?
答案
(1)P、Q通过弹簧发生碰撞,当两滑块速度相等时,弹簧压缩到最短,弹性势能最大,设此时共同速度为v,对P、Q(包括弹簧)组成的系统,由动量守恒定律有:
mv0=(m+m)v
解得:v=
v0=m m+m
v01 2
(2)在压缩弹簧的过程中,系统中只有弹簧弹力做功,系统满足机械能守恒条件即系统机械能守恒
所以弹簧增加的弹性势能等于系统减少的动能
即:Epm=
mv02-1 2
(m+m)v21 2
代入v=
可得:v0 2
Epm=
mv021 4
答:(1)当弹簧压缩最短时Q的速度为v0 2
(2)弹簧具有的最大弹性势能等于
m1 4
.v 20
