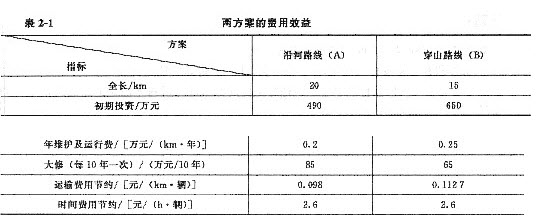
某市修建一条快速干线,初步拟定两条备选路线,即沿河路线与穿山路线,两条路线的平均车速都提高了50 km/h,日平均流量都是6000辆,寿命均为30年,且无残值,基准收益率为12%,其他数据见表2-1。
已知(P/F,12%,10)=0.3220,(P/F,12%,20)=0.1037,(A/P,12%,30)=0.1241。
问题:
试用生命周期费用理论分析两条路线的优劣,并作出方案选择(计算结果保留两位小数)。
参考答案:
(1)计算沿河路线方案的费用效率(CE)。
①求系统效率(SE)。
时间费用节约=6000×365×20/50×2.6/10000=227.76(万元/年)
运输费用节约=6000×365×20×0.098/10000=429.24(万元/年)
则:SE=227.76+429.24=657(万元/年)
②求生命周期费用(LCC),包括设置费(IC)和维持费(SC)。
a.IC=490(A/P,12%,30)
=490×0.1241
=60.81(万元/年)
b.SC=0.2×20+[85(P/F,12%,10)+85(P/F,12%,20)](A/P,12%,30)
=4+(85×0.3220+85×0.1037)×0.1241
=8.49(万元/年)
则:LCC=IC+SC=60.81+8.49=69.3(万元/年)
③求费用效率(CE)。
CE=SE/LCC=657/69.3=9.48
(2)计算穿山路线方案的费用效率(CE)。
①求系统效率(SE)。
时间费用节约=6000×365×15/50×2.6/10000=170.82(万元/年)
运输费用节约=6000×365×15×0.1127/10000=370.22(万元/年)
则:SE=170.82+370.22=541.04(万元/年)
②求生命周期费用(LCC),包括设置费(IC)和维持费(SC)。
a.IC=650(A/P,12%,30)
=650×0.1241
=80.67(万元/年)
b.SC=0.25×15+[65(P/F,12%,10)+65(P/F,12%,20)](A/P,12%,30)
=3.75+(65×0.3220+65×0.1037)×0.1241
=7.18(万元/年)
则:LCC=1C+SC=80.67+7.18=87.85(万元/年)
③求费用效率(CE)。
CE=SE/LCC=541.04/87.85=6.16
(3)方案选择。
因为沿河路线方案的费用效率大于穿山路线方案的费用效率,所以选择沿河路线方案。
