问题
解答题
(1)对于任意给定的一个矩形C,是否存在另一个矩形,使它的周长和面积都是矩形C的2倍?请说明你理由。(3分)
(2)当实数m是什么值时,对于任何一个矩形C,都存在另一个矩形,它的周长与面积都是矩形C的m倍?证明你的结论。(7分)
答案
（1）理由见解析(2) 当m≥1时,所有的矩形都有周长与面积都是已知矩形的m倍的矩形，证明见解析
（1）设已知矩形的长与宽分别为a,b,所求矩形为x,y.
则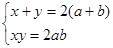
∴x,y是方程t2－2(a+b)t+2ab=0的两根
∵⊿=4(a+b)2－8ab=4(a2+b2)＞0, ∴方程有解
∴对于长与宽分别为a,b矩形,存在周长与面积都是已知矩形的2倍的矩形。(3分)
(2)设已知矩形的长与宽分别为a,b,所求矩形为x,y.
则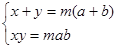
∴x,y是方程t2－m(a+b)t+mab=0的两根
当⊿=m2(a+b)2－4mab＞0,即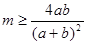
时,方程有解
∴对于长与宽分别为a,b矩形, 当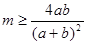时,存在周长与面积都是已知矩形的m倍的矩形 (7分)
∵(a－b)2≥0, ∴a2+b2≥2ab ∴a2+b2+2ab≥4ab 即(a+b)2≥4ab,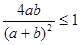
,
∴
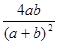的最大值为1 (9分)
∴当m≥1时,所有的矩形都有周长与面积都是已知矩形的m倍的矩形。
本题考查了一元二次方程根的判别式的应用；（1）由题意可知：分别设出已知矩形和所求矩形的长与宽，再根据周长和面积的关系可以列出两个关系式，观察两个关系式可得一个根为xy的一元二次方程，再根据判别式可以确定方程是否有解，进而确定所求矩形是否存在；（2）方法与（1）一样．