问题
解答题
| 某商场经销甲、乙两种商品，甲种商品每件进价15元，售价20元；乙种商品每件进价35元，售价45元。（1）若该商场同时购进甲、乙两种商品共100件，恰好用去2700元，则购进的甲、乙两种商品各多少件？ （2）若该商场用不超过5050元同时购进甲、乙两种商品共200件，且购进甲种商品的数量不超过乙种产品。请你帮助该商场设计相应的进货方案并求出哪种进货方案获利（利润=售价-进价）最多，最多获利是多少？ （3）在“五一”黄金周期间，该商场对甲、乙两种商品进行如下优惠促销活动： | ||||||||
|
答案
解：（1）设购进甲种商品x件，乙种商品y件，根据题意列方程
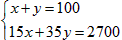，解这个方程组，得
，
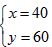所以，购进的甲种商品40件，乙两种商品60件；
（2）设购进甲种商品a件，则购进乙种商品（200-a）件，由题意得
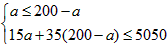，解这个不等式组，得97.5≤a≤100，
因为a为整数，所以，a=98，99，100，此时200-a=102，101，100，
所以商场可购进甲种商品98件、乙种商品102件，或甲种商品99件、乙种商品101件，甲种商品100件、乙种商品100件，
商场获利W=（20-15）a+（45-35）（200-a）=-5a+2000
∵-5＜0，∴W随a的增大而减小，当a取最小值98时，W最大，且最大值为1510；
（3）根据题意，第一天只购买300元的甲种商品，不享受优惠条件，所以200÷20=10（件），第二天只购买乙种商品，有以下两种情况：情况一，购买乙种商品打九折，324÷90%÷45=8（件）；情况二，购买乙种商品打八折，324÷80%÷45=9（件）。所以，一共可购买甲、乙两种商品18或19件。