问题
填空题
设矩阵A=
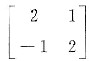，E为二阶单位矩阵，矩阵B满足BA=B+2E，则|B|=______．
答案
参考答案：B
解析：[考点提示] 行列式、矩阵的计算．
[解题分析] 由已知BA=B+2E，有B(A-E)=2E，两边取行列式，得
|B|·|A-E|=4．
因为|A-E|=[*]=2，所以|B|=2．
搜题请搜索小程序“爱下问搜题”
设矩阵A=
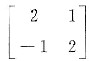，E为二阶单位矩阵，矩阵B满足BA=B+2E，则|B|=______．
参考答案：B
解析：[考点提示] 行列式、矩阵的计算．
[解题分析] 由已知BA=B+2E，有B(A-E)=2E，两边取行列式，得
|B|·|A-E|=4．
因为|A-E|=[*]=2，所以|B|=2．