问题
问答题
设函数f(x)在(-∞，+∞)上有定义，在区间[0，2]上，f(x)=x(x2-4)．若对任意的x都满足f(x)=kf(x+2)，其中k为常数．
(1) 写出f(x)在[-2，0]上的表达式．
(2)问k为何值时，f(x)在x=0处可导．
答案
参考答案：由题设，f(x)=x(x2-4)，x∈[0，2]．
当x∈[-2，0)时，x+2∈[0，2)，则由f(x)=kf(x+2)知
f(x)=kf(x+2)=k(x+2)[(x+2)2-4]
=k(x+2)(x2+4x)=kx(x+2)(x+4)，x∈[-2，0)．
由导数定义及f(0)=0．
有
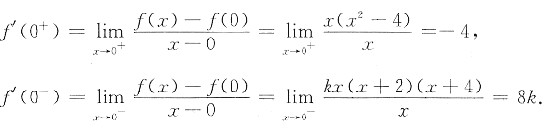
令f’(0+)=f’(0-)，则k=-
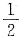．所以当k=-
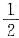时，f(x)在x=0处可导．
解析：[考点提示] 分段函数、导数的定义．