问题
填空题
设函数f(x)与g(x)在点x=0的某邻域可求任意阶导数，且满足f"(x)+f’(x)g(x)+f(x)x=ex-1，f(0)=1，f’(0)=0，
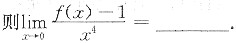
答案
参考答案：
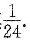
解析：
[分析]： 由f(0)=1，f’(0)=0及所给式子，有f"(0)=0，再求导有f’"(0)=0，f(4)(0)=1，由洛比达法则，有
[*]
搜题请搜索小程序“爱下问搜题”
设函数f(x)与g(x)在点x=0的某邻域可求任意阶导数，且满足f"(x)+f’(x)g(x)+f(x)x=ex-1，f(0)=1，f’(0)=0，
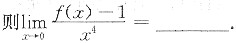
参考答案：
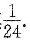
解析：
[分析]： 由f(0)=1，f’(0)=0及所给式子，有f"(0)=0，再求导有f’"(0)=0，f(4)(0)=1，由洛比达法则，有
[*]