如图，两个带同种电荷的小球A和B，A、B的质量分别为m和2m．开始

问题问答题

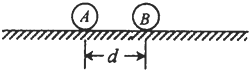
如图，两个带同种电荷的小球A和B，A、B的质量分别为m和2m．开始时将它们固定在绝缘的光滑水平面上保持静止，A、B相距为d．A、B间的相互作用为遵守牛顿第三定律．现同时释放A、B，经过一段时间，A、B相距2d，此时B的速度大小为v．

求：（1）此时A的速度大小．

（2）此过程中B对A做的功．

（3）此过程中A球移动的距离．

答案

（1）以A、B为研究对象，由动量守恒定律 m_Av_A=m_Bv

求出v_A=2v

（2）对A，由动能定理，得到：

=2mv2

（3）由于两个球的合力相等，故加速度之比等于质量之比的倒数，为2：1；由于初速度为零，故任意时刻速度之比等于加速度之比，为2：1；故全程的平均速度之比为2：1；故位移之比为2：1，即：

其中：s_A+s_B=d

联立求解得到：s_A=

答：（1）此时A的速度大小为2v．

（2）此过程中B对A做的功为2mv²．

（3）此过程中A球移动的距离为

．