问题
问答题
试求椭圆C：
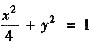在点P1(0，1)与P2(2，0)处的曲率与曲率圆方程．
答案
参考答案：因点P1(0，1)在上半椭圆[*]上，从而
[*]
由此可得椭圆C在点P1处的曲率[*]，曲率圆的半径R1=4．由于椭圆C在点P1处的切线为y=1，法线即为y轴，所以C在点P1处的曲率圆中心在y轴上点P1下方与点P1距离为4处，即曲率圆中心为O1(0，-3)，曲率圆方程为x2+(y+3)2=16．
同理，因点P2(0，2)在右半椭圆[*]上，从而
[*]
故椭圆C在点P2处的曲率[*]，曲率圆的半径[*]由于椭圆C在点P2处的切线方程为x=2，法线即为x轴，所以C在点P2处的曲率圆中心在x轴上点P2左方与点P2距离为[*]处，即曲率圆中心为O2[*]曲率圆的方程为[*]