问题
解答题
已知函数f(x)=cos2x+
①求f(x)的最小正周期及其单调区间; ②当x取何值时,f(x)取最大值?最大值是多少? ③在直角坐标系内,画出f(x)在一个周期内的图象. |
答案
f(x)=cos2x+
sin2x=2sin(2x+3
),π 6
①∵ω=2,∴f(x)的最小正周期T=
=π;2π 2
其单调增区间为2kπ-
≤2x+π 2
≤2kπ+π 6
,k∈Z,π 2
即:kπ-
≤x≤kπ+π 3
,k∈Z,π 6
则f(x)的单调减区间是[kπ-
,kπ+π 3
],k∈Z;π 6
②当2x+
=2kπ+π 6
,k∈Z,即x=kπ+π 2
,k∈Z时,f(x)取最大值,最大值为2;π 6
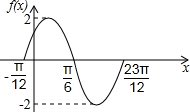
③在直角坐标系内,画出f(x)在一个周期内的图象,如图所示;