问题
问答题
设物体由一圆锥以及与这一圆锥共底的半球拼成，而锥的高等于其底半径a，求此物体对对称轴的转动惯量(设物体密度μ=1)．
答案
参考答案：解法一 选取坐标系，使原点在锥顶，如图1—8—2，半球面与锥面的方程分别为z=a+
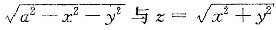，于是对称轴为z轴，所求的转动惯量为
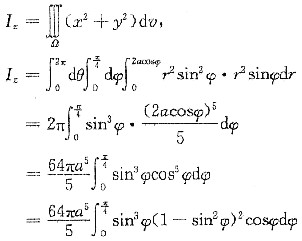
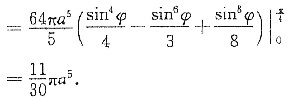
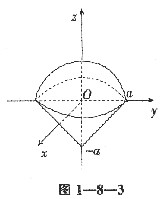
解法二 选取坐标系，使原点在球心，如图1—8—3，半球面与锥面的方程分别为
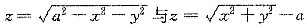，对称于z轴．采用球面坐标，于是半球对于z轴的转动惯量为
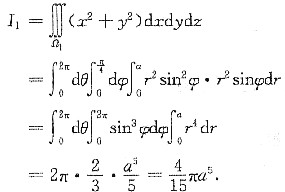
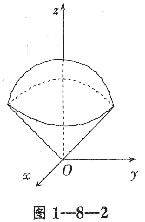
锥体对于z轴的转动惯量为(采用柱面坐标)
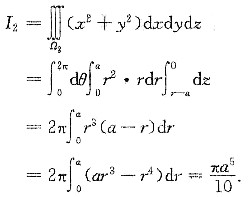
因此，物体对于z轴的转动惯量为
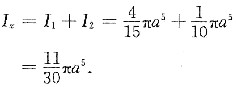
解析：
[分析]： 这是三重积分的应用题，适当建立坐标系，按照转动惯量的计算公式求解．