问题
解答题
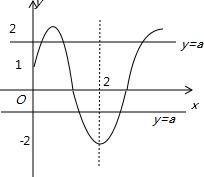
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
(1)求f(x)的解析式; (2)求方程f(x)=a存在于[0,7/2]上的解的和,其中a为满足-2<a<2的已知常数. |
答案
(1)函数f(x)=Asin(ω+φ)(A>0,ω>0,|φ|<
)的图象在y轴上的截距为1,π 2
在相邻最值点(x0,2),[x0+
,-2](x0>0)上f(x)分别取得最大值和最小值.3 2
所以A=2,T=3,ω=
,(0,1)在函数图象上,2π 3
所以1=2sinφ,φ=
所以函数的解析式:f(x)=2sin(π 6
x+2π 3
)π 6
(2)当-2<a<1时,方程f(x)=a存在于[0,
]上的解的和为4,7 2
当1≤a<2时:由2sin(
x+2π 3
)=aπ 6
解得x=
arcsin3 2π
-a 2
=π 6
arcsin3 2π
-a 2
×π 6
解的和为:3 2π
+15 4
arcsin3 2π a 2
