问题
问答题
已知可行域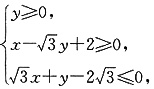
的外接圆C与x轴交于点A1、A2，椭圆C1以线段A1A2为长轴，离心率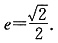
(1)求圆C及椭圆C1的方程；
(2)设椭圆C1的右焦点为F，点P为圆C上异于A1、A2的动点，过原点O作直线PF的垂线交直线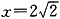
于点Q，判断直线PQ与圆C的位置关系，并给出证明，
答案
参考答案：
(1)由题意可知，可行域是以A1(-2，0)、A2(2，0)及点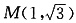
为顶点的三角形，
∵A1M⊥A2M，∴△A1A2M为直角三角形，
∴外接圆C以原点O为圆心，线段A1A2为直径，故其方程为x2+y2=4
∵2a=4，∴a=2．又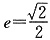
，∴
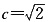，可得
∴所求椭圆C1的方程是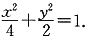
(2)椭圆C1的右焦点为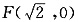
设点P的坐标为(m，n)，(n≠0，m≠2，-2)．
①当直线PF斜率不存在时，P点坐标为
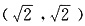或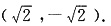
∴过原点O作直线PF的垂线交直线
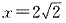于点Q，点Q坐标为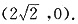
则k(PQ)=-1或1，PQ方程为：
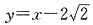或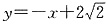
则圆心(0，0)到PQ直线的距离都为d=2=r
∴直线PQ与圆C相切
②当直线PF斜率存在时，则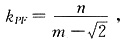
过原点O作直线PF的垂线斜率为：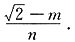
∴过原点O作直线PF的垂线方程为：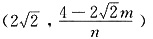
联立方程：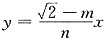
①，
②
解得：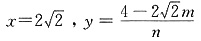
∴点Q的坐标为
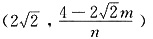
又点P(m，n)在圆上，∴n2-4=m2
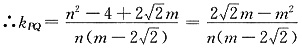
又直线OP的斜率为：
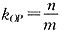
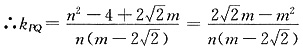
∵P为圆的半径的端点且PQ⊥OP
∴直线PQ与圆C的相切
综上所述：直线PQ与圆C相切．
