问题
问答题
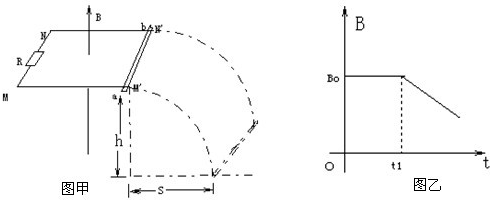
在水平面内的光滑平行导轨MM′、NN′长度为L,它们之间距离也是L,定值电阻R连接MN,导轨平面距地面高为h.在导轨所处空间有以M′N′为边界的竖直向上的匀强磁场.将长度为L,电阻为r的金属棒ab放在导轨M′N′端并使其恰好处在磁场的边界线内,如图甲所示.已知磁场与时间的关系如图乙所示(0<t<t1,B=Bo;t≥t1,B=B0-kt).t1时刻磁场的减弱,使棒ab突然掉落在离轨道末端S远处的地面上.求金属棒抛离磁场瞬间回路的电热功率P.轨道电阻不计,重力加速度为g.
答案
设回路电流为i,所求电功率为P=i2(R+r)
由于i=
,e-BoLv R+r
式中e=L2
=L2k为B变化引起的感应电动势.△B △t
BoLv为棒切割磁感线引起的电动势,v=sg 2h
则金属棒抛离磁场瞬间回路的电热功率P=
.(L2k-BoLs
)2g 2h R+r
答:金属棒抛离磁场瞬间回路的电热功率P=
.(L2k-BoLs
)2g 2h R+r
