问题
解答题
设函数f(x)=sinxcosx-
(I)求f(x)的最小正周期; (II)若函数y=f(x)的图象按
|
答案
(I)∵f(x)=sinxcosx-
cos(x+π)cosx3
=sinxcosx+
cosxcosx3
=
sin2x+1 2
cos2x+3 2 3 2
=sin(2x+
)+π 3 3 2
∴f(x)的最小正周期T=
=π2π 2
(II)∵函数y=f(x)的图象按
=(b
,π 4
)平移后得到的函数y=g(x)的图象,3 2
∴g(x)=sin(2x+
-π 3
)+π 2
+3 2
=sin(2x-3 2
)+π 6 3
∵0<x≤
∴-π 4
<2x-π 6
≤π 6
,π 3
∴y=g(x)在(0,
]上的最大值为:π 4
.3 3 2

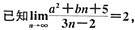 则a,b等于().
则a,b等于().