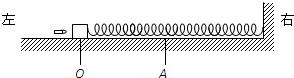
如图所示,水平面上OA部分粗糙,其他部分光滑.轻弹簧一端固定,另一端与质量为M的小滑块连接,开始时滑块静止在O点,弹簧处于原长.一质量为m的子弹以大小为v的速度水平向右射入滑块,并留在滑块中,子弹打击滑块的时间极短,可忽略不计.之后,滑块向右运动并通过A点,返回后恰好停在出发点O处.求:
(1)子弹打击滑块结束后的瞬间,滑块和子弹的共同速度大小;
(2)试简要说明滑块从O到A及从A到O两个过程中速度大小的变化情况,并计算滑块滑行过程中弹簧弹性势能的最大值;
(3)滑块停在O点后,另一颗质量也为m的子弹以另一速度水平向右射入滑块并停留在滑块中,此后滑块运动过程中仅两次经过O点,求第二颗子弹的入射速度u的大小范围.
(1)子弹打击滑块,满足动量守恒定律,设子弹射入滑块后滑块的速度为v1,
则:mv=(M+m)v1
v1=
…①mv M+m
(2)从O到A滑块做加速度增大的减速运动,从A到O滑块可能做加速度增大的减速运动,或先做加速度减小的加速运动再做加速度增大的减速运动.
滑块向右到达最右端时,弹簧的弹性势能最大.设在OA段克服摩擦力做的功为Wf,与滑块的动摩擦因数为μ,弹性势能最大值为Ep,
根据能量守恒定律:
(M+m)1 2
=Wf+Ep…②v 21
由于滑块恰能返回到O点,返回过程中,根据能量守恒定律:
Ep=Wf…③ ①②③式解得:Ep= m2v2 4(M+m)
(3)设第二颗子弹射入滑块后滑块的速度为v2,由动量守恒定律得:mu=(M+2m)v2 …④
如果滑块第一次返回O点时停下,则滑块的运动情况同前,对该过程应用能量守恒定律:
(M+2m)1 2
=2W′f⑤v 22
=W′f Wf
…⑥M+2m M+m
①②③④⑤⑥联立解得:u1=
vM+2m M+m
如果滑块第三次返回O点时停下,对该过程由能量守恒:
(M+2m)v1 2
=4W′f⑦′ 22
①②③④⑥⑦联立解得:u2=2
vM+2m M+m
所以,滑块仅两次经过O点,第二颗子弹入射速度的大小范围在:
v<u<M+2m M+m 2
vM+2m M+m
答:(1)子弹打击滑块结束后的瞬间,滑块和子弹的共同速度大小是
;mv M+m
(2)滑块滑行过程中弹簧弹性势能的最大值是
; m2v2 4(M+m)
(3)第二颗子弹的入射速度u的大小范围是
v<u<M+2m M+m 2
v.M+2m M+m
