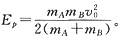参考答案：

教学重点：用动量守恒定律、机械能守恒定律讨论碰撞问题。

教学难点：对各种碰撞问题的理解。

教学方法：教师启发、引导，学生讨论、交流。

教学用具：投影片，多媒体辅助教学设备。

教学过程：

(一)引入新课

碰撞过程是物体之间相互作用时间非常短暂的一种特殊过程，因而碰撞过程中动量守恒。

提问：(1)守恒的原因是什么(因相互作用时间短暂，因此一般满足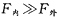的条件)

(2)碰撞过程中，物体没有宏观的位移，但每个物体的速度可在短暂的时间内发生改变。

(3)碰撞过程中，系统的总动能只能不变或减少，不可能增加。

(4)碰撞中，总动能减少最多的情况是什么(在发生完全非弹性碰撞时总动能减少最多)

(二)进行新课

1．展示投影片1，内容如下：

如图所示，质量为M的重锤自h高度由静止开始下落，砸到质量为m的木楔上没有弹起，二者一起向下运动。设地层给它们的平均阻力为F，则木楔可进入的深度L是多少

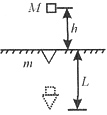
组织学生认真读题，并给三分钟时间思考。

(1)提问学生解题方法：可能出现的错误是：认为过程中只有地层阻力F做负功使机械能损失，因而解之为

Mg(h+L)+mgL-FL=0

(2)归纳：第一阶段，M做自由落体运动机械能守恒，m不动，直到M开始接触m为止。再下面一个阶段，M与m以共同速度开始向地层内运动，阻力F做负功，系统机械能损失。

提问：第一阶段结束时，M有速度，，而m速度为零。下一阶段开始时，M与m就具有共同速度，即m的速度不为零了，这种变化是如何实现的呢(在上述前后两个阶段中间，还有一个短暂的阶段，在这个阶段中，M和m发生了完全非弹性碰撞，这个阶段中，机械能是有损失的)

(3)让学生独立地写出完整的方程组

第一阶段，对重锤有：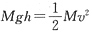

第二阶段，对重锤及木楔有：Mv+0=(M+m)v’

第三阶段，对重锤及木楔有：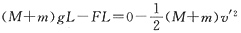

(4)小结：在这类问题中，没有出现碰撞两个字，碰撞过程是隐含在整个物理过程之中的，在做题中，要认真分析物理过程，发掘隐含的碰撞问题。

2．展示内容如下：

如图所示，在光滑水平地面上，质量为M的滑块上用轻杆及轻绳悬吊质量为m的小球，此装置一起以速度v₀向右滑动，另一质量也为M的滑块静止于上述装置的右侧。当两滑块相撞后，便粘在一起向右运动，则小球此时的运动速度是多少

(1)提问学生解答方案。可能出现的错误有：在碰撞过程中水平动量守恒，设碰后共同速度为v，则有：

(M+m)v₀+0=(2M+m)v

解得：小球速度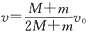

(2)明确表示此种解法是错误的。提醒学生注意碰撞的特点：即宏观没有位移，速度发生变化，然后要求学生们寻找错误的原因。

(3)归纳：

明确以下的研究方法：

①碰撞之前滑块与小球做匀速直线运动，悬线处于竖直方向。

②两个滑块碰撞时间极其短暂，碰撞前、后瞬间相比，滑块及小球的宏观位置都没有发生改变，因此悬线仍保持竖直方向。

③碰撞前后悬线都保持竖直方向，因此碰撞过程中，悬线不可能给小球以水平方向的作用力，因此小球的水平速度不变。

④结论是：小球未参与滑块之间的完全非弹性碰撞，小球的速度保持为v₀。

小结：由于碰撞中宏观无位移，所以在有些问题中，不是所有物体都参与了碰撞过程，在遇到具体问题时一定要注意分析与区别。

3．展示内容如下：

在光滑水平面上，有A、B两个小球向右沿同一直线运动，取向右为正，两球的动量分别是p_A=5kg·m/s，p_B=7kg·m/s，如图所示，若能发生正碰，则碰后两球的动量增量Δp_A、Δp_B可能是()。

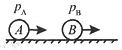
A．Δp_A=-3kg·m/s；Δp_B=3kg·m/s

B．Δp_A=3kg·m/s；Δp_B=3kg·m/s

C．Δp_A=-10kg·m/s；Δp_B=10kg·m/s

D．Δp_A=3kg·m/s；Δp_B=-3kg·m/s

(1)提问：解决此类问题的依据是什么

归纳：①系统动量守恒；②系统的总能量不能增加；③系统总能量的减少量不能大于发生完全非弹性碰撞时的能量减少量；④碰撞中每个物体动量的增量方向一定与受力方向相同；⑤如碰撞后向同方向运动，则后面物体的速度不能大于前面物体的速度。

(2)提问：题目仅给出两球的动量，如何比较碰撞过程中的能量变化(帮助学生回忆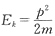的关系)

(3)提问：题目没有直接给出两球的质量关系，如何找到质量关系

要求学生认真读题，挖掘隐含的质量关系，即A追上B并相碰撞，

所以：v_A＞v_B，即最后得到正确答案为A。

4．展示内容如下：

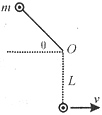
如图所示，质量为m的小球被长为L的轻绳拴住，轻绳的一端固定在O点，将小球拉到绳子拉直并与水平面成θ角的位置上，将小球由静止释放，则小球经过最低点时的即时速度是多大组织学生认真读题，并给三分钟思考时间。

(1)提问学生解答方法。可能出现的错误有：认为轻绳的拉力不做功，因此过程中机械能守恒，以最低点为重力势能的零点，则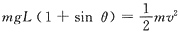：，得。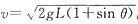

(2)引导学生分析物理过程

第一阶段，小球做自由落体运动，直到轻绳位于水平面以下，与水平面成θ角的位置处为止。在这一阶段，小球只受重力作用，机械能守恒成立。

下一阶段，轻绳绷直，拉住小球做竖直向上的圆周运动，直到小球到最低点，在此过程中，轻绳拉力不做功，机械能守恒成立。

提问：在第一阶段终止的时刻，小球的瞬时速度是什么方向在下一阶段初始的时刻，小球的瞬时速度是什么方向

在学生找到这两个速度方向的不同后，要求学生解释其原因，总结归纳学生的解释，明确以下观点：

在第一阶段终止时刻，小球的速度竖直向下，既有沿下一步圆周运动轨道切线方向(即与轻绳相垂直的方向)的分量，又有沿轨道半径方向(即沿轻绳方向)的分量。在轻绳绷直的一瞬间，轻绳给小球一个很大的冲量，使小球沿绳方向的动量减小到零，此过程类似于悬挂轻绳的物体(例如天花板)与小球在沿绳的方向上发生了完全非弹性碰撞，由于天花板的质量无限大(相对小球)，因此碰后共同速度趋向于零。在这个过程中，小球沿绳方向分速度所对应的一份动能全部损失了。因此，整个运动过程按机械能守恒来处理就是错误的。

(3)要求学生重新写出正确的方程组

解得：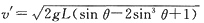

小结：很多实际问题都可以类比为碰撞，建立合理的碰撞模型可以很简洁直观地解决问题，下面继续看例题。

5．展示内容如下：

如图所示，质量分别为m_A和m_B的滑块之间用轻质弹簧相连，水平地面光滑，m_A、m_B原来静止，在瞬间给m_B一很大的冲量，使m_B获得初速度v₀，则在以后的运动中，弹簧的最大势能是多少

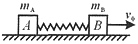
(1)m_A、m_B与弹簧所构成的系统在下一步运动过程中能否类比为一个m_A、m_B发生碰撞的模型(因系统水平方向动量守恒，所以可类比为碰撞模型)

(2)当弹性势能最大时，系统相当于发生了什么样的碰撞(势能最大，动能损失就最大，因此可建立完全非弹性碰撞模型)经过讨论，得到正确结论以后，要求学生据此而正确解答问题，得到结果为：