问题
解答题
已知f是直角坐标平面xOy到自身的一个映射,点P在映射f下的象为点Q,记作Q=f(P).设P1(x1,y1),P2=f(P1),P3=f(P2),…,Pn=f(Pn-1),….如果存在一个圆,使所有的点Pn(xn,yn)(n∈N*)都在这个圆内或圆上,那么称这个圆为点Pn(xn,yn)的一个收敛圆.特别地,当P1=f(P1)时,则称点P1为映射f下的不动点.若点P(x,y)在映射f下的象为点Q(-x+1,
(Ⅰ)求映射f下不动点的坐标; (Ⅱ)若P1的坐标为(2,2),求证:点Pn(xn,yn)(n∈N*)存在一个半径为2的收敛圆. |
答案
(Ⅰ)设不动点的坐标为P0(x0,y0),
由题意,得
,解得x0=x0=-x0+1 y0=
y01 2
, y0=0,1 2
所以此映射f下不动点为P0(
, 0).1 2
(Ⅱ)证明:由Pn+1=f(Pn),得
,xn+1=-xn+1 yn+1=
yn1 2
所以xn+1-
=-(xn-1 2
), yn+1=1 2
yn,1 2
因为x1=2,y1=2,
所以xn-
≠0, yn≠0,1 2
所以
=-1, xn+1- 1 2 xn- 1 2
=yn+1 yn
,1 2
由等比数列定义,得数列{xn-
}(n∈N*)是公比为-1,首项为x1-1 2
=1 2
的等比数列,3 2
所以xn-
=1 2
×(-1)n-1,则xn=3 2
+(-1)n-1×1 2
.3 2
同理yn=2×(
)n-1.1 2
所以Pn(
+(-1)n-1×1 2
, 2×(3 2
)n-1).1 2
设A(
, 1),则|APn|=1 2
,(
)2+[1-2×(3 2
)n-1]21 2
因为0<2×(
)n-1≤2,1 2
所以-1≤1-2×(
)n-1<1,1 2
所以|APn|≤
<2.(
)2+13 2
故所有的点Pn(n∈N*)都在以A(
, 1)为圆心,2为半径的圆内,1 2
即点Pn(xn,yn)存在一个半径为2的收敛圆.

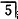 缺失,固定义齿修复后,自觉觉胀痛不适,伴口臭。查:
缺失,固定义齿修复后,自觉觉胀痛不适,伴口臭。查: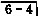 固定桥完整,无松动,无叩痛。7l近中邻面有浅龋洞,与
固定桥完整,无松动,无叩痛。7l近中邻面有浅龋洞,与 中面呈楔状缝隙,探诊无明显酸痛,牙髓活力测正常,无叩痛,无松动。
中面呈楔状缝隙,探诊无明显酸痛,牙髓活力测正常,无叩痛,无松动。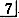 近中龈 * * 红肿,有触痛,可见食物嵌塞
近中龈 * * 红肿,有触痛,可见食物嵌塞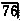 * * 炎
* * 炎