问题
解答题
求直线l1:2x+y-4=0关于l:3x+4y-1=0对称的直线l2的方程.
答案
2x+11y+16=0.
设点A(x,y)是直线l2上任意一点，它关于l的对称点为A′(x0,y0)，则
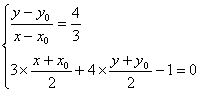
解得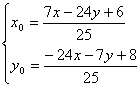
∵A′点(x0,y0)在直线l1:2x+y-4=0上，
∴
,
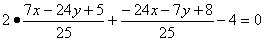化简得2x+11y+16=0.
搜题请搜索小程序“爱下问搜题”
求直线l1:2x+y-4=0关于l:3x+4y-1=0对称的直线l2的方程.
2x+11y+16=0.
设点A(x,y)是直线l2上任意一点，它关于l的对称点为A′(x0,y0)，则
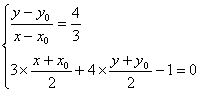
解得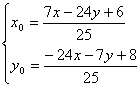
∵A′点(x0,y0)在直线l1:2x+y-4=0上，
∴,
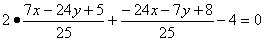化简得2x+11y+16=0.