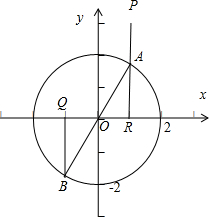
∵已知圆O：x²+y²=4，AB为圆O的任意一条直径，P（1，3），Q（-1，0），

设点R（1，0）、点A（x，y），

则点B（-x，-y），PA+AB+BQ=

(x-1)2+(y-3)2

+4+

(-x+1)2+y2

=

(x-1)2+(y-3)2

+

(x-1)2+y2

+4=PA+AR+4．

由于

(x-1)2+(y-3)2

表示圆上的点A（x，y）到点P（1，3）的距离，

而

(x-1)2+y2

表示圆上的点A（x，y）到点R（1，0）的距离，

故当点A是PR与圆的交点时，PA+AR=

(x-1)2+(y-3)2

+

(x-1)2+y2

最小，

即PA+AB+BQ最小，此时，点A（1，

3

），故AB的斜率为

3 -0

1-0

=

3

，

故直线AB的方程为 y=

3

x，

故答案为 y=

3

x．