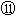如图所示,某货场需将质量为m1=100kg的货物(可视为质点)从高处运送至地面,为避免货物与地面发生撞击,现利用固定于地面的光滑四分之一圆轨道,使货物由轨道顶端无初速滑下,轨道半径R=1.8m。地面上紧靠轨道依次排放两块完全相同的木板A、B,长度均为l=2m,质量均为m2=100kg,木板上表面与轨道末端相切。货物与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数μ2=0.2。(最大静摩擦力与滑动摩擦力大小相等,取g=10 m/s2)
(1)求货物到达圆轨道末端时对轨道的压力。
(2)若货物滑上木板A时,木板不动,而滑上木板B时,木板B开始滑动,求μ1应满足的条件。
(3)若μ1=0.5,求货物滑到木板A末端时的速度和在木板A上运动的时间。
解:(1)设货物滑到圆轨道末端时的速度为v0,对货物的下滑过程,
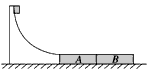
根据机械能守恒定律得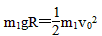 ①
①
设货物在轨道末端所受支持力的大小为FN,根据牛顿第二定律得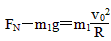 ②
②
联立①②式,代入数据得 FN=3000N③
根据牛顿第三定律,货物对轨道的压力大小为3000N,方向竖直向下。
(2)若滑上木板A时,木板不动,由受力分析得 μ1m1g≤μ2(m1+2m2)g④
若滑上木板B时,木板B开始滑动,由受力分析得 μ1m1g>μ2(m1+m2)g⑤
联立④⑤式,代入数据得 0.4<μ1≤0.6⑥
(3)μ1=0.5,由⑥式可知,货物在木板A上滑动时,木板不动。
设货物在木板A上做减速运动时的加速度大小为a1,由牛顿第二定律得μ1m1g=m1a1⑦
设货物滑到木板A末端时的速度为v1,由运动学公式得v12-v02=-2a1l⑧
联立①⑦⑧式,代入数据得v1=4m/s⑨
设在木板A上运动的时间为t,由运动学公式得v1=v0-a1t⑩
联立①⑦⑨⑩式,代入数据得t=0.4s