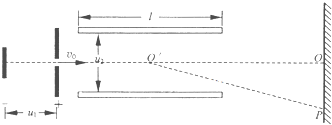
如图所示为电子显示仪器(如示波器)的核心部件.如图所示,左边部分为加速装置,阴极产生的热电子(电荷量为e,质量为m)由静止开始经加速电压μ1加速后,进入板长为l,间距为d,直流电压为μ2的偏转电场区域,偏转区域右侧为荧光屏,电子轰击荧光屏能够显示出光斑P.依据上述信息,求:
(l)电子离开加速电场时的速度大小;
(2)电子离开偏转电场时的速度与进入时速度的夹角的正切值;
(3)若把某时刻做为计时起点t=0,从该时刻起显示屏由静止开始向左做加速度为a的匀加速直线运动,试定量说明光斑在屏上的运动性质.
(1)电子在加速电场中,根据动能定理得,eu1=
mv2;①1 2
则得:v=
②2eu1 m
(2)电子在偏转电场中运动的时间 t=
③l v
加速度 a=
=eE m
④eu2 md
电子离开偏转电场时竖直分速度大小 vy=at ⑤
在偏转电场中的偏转角的正切 tanθ=
⑥vy v
联立②③④⑤⑥得:tanθ=u2l 2u1d
(3)光屏在t时间内向左运动的位移 x=
at21 2
光斑在竖直方向的位移 y=xtanθ=
at2•1 2
=u2l 2u1d
(1 2
)t2u2la 2u1d
可知光斑在竖直方向上做初速度为0、加速度为
的匀加速直线运动.u2la 2u1d
答:
(l)电子离开加速电场时的速度大小为
;2eu1 m
(2)电子离开偏转电场时的速度与进入时速度的夹角的正切值为
;u2l 2u1d
(3)光斑在竖直方向上做初速度为0、加速度为
的匀加速直线运动.u2la 2u1d
