问题
计算题
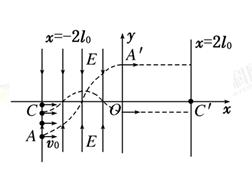
如图所示的直角坐标系中，在直线x＝－2l0到y轴区域内存在着两个大小相等、方向相反的有界匀强电场，其中x轴上方的电场方向沿y轴负方向，x轴下方的电场方向沿y轴正方向。在电场左边界上A(－2l0，－ l0)到C(－2l0，0)区域内，连续分布着电荷量为＋q、质量为m的粒子。从某时刻起由A点到C点间的粒子，依次连续以相同的速度v0沿x轴正方向射入电场。若从A点射入的粒子，恰好从y轴上的A′(0，l0)沿x轴正方向射出电场，其轨迹如图虚线所示。不计粒子的重力及它们间的相互作用。求
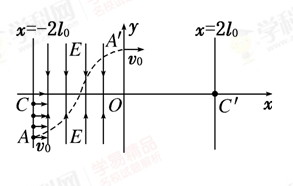
（1）粒子从A点到A′的时间t；
（2) 匀强电场的电场强度E；
（3）在AC间还有哪些位置的粒子，通过电场后也能沿x轴正方向运动？
答案
（1）T=
；（2）E＝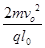
；（3）AC间坐标为y＝－
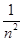l0 (n＝1，2，3…)的点通过电场后也能沿x轴正方向运动
题目分析: (1)从A′点射出的粒子，由A到A′的运动时间为T，粒子x轴方向匀速直线运动
2l0＝v0T， 解得T=
(2)由运动的对称性知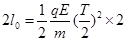 
解得：E＝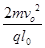
(3)设到C点距离为Δy处射出的粒子通过电场后也沿x轴正方向运动，粒子第一次到达x轴用时为Δt，水平位移为Δx。
则Δx＝v0Δt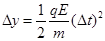 
若满足2l0＝n·2Δx(n＝1，2，3…)，则粒子从电场射出时的速度方向也将沿x轴正方向运动(如图所示)。
解得：Δy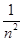＝l0(n＝1，2，3…)
即AC间坐标为y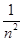＝－l0 (n＝1，2，3…)的点通过电场后也能沿x轴正方向运动。