问题
计算题
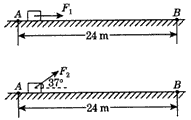
如图所示，水平地面上有一质量m=11.5 kg的物块，在F1=57.5 N的水平力作用下，由静止开始运动，经t=4 s时的位移x=24 m。
（1）求物块与地面之间的动摩擦因数μ；
（2）如果从A点起，物块在斜向上、与水平方向成37°角、大小为75 N的拉力F2作用下运动，作用一段时间后撤去F2，要使物块能到达B点，F2作用的最短时间是多少？（g取10 m/s2）
答案
解：（1）由运动学公式得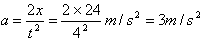
由牛顿第二定律有：F1-μmg=ma
解得：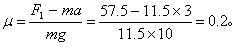
（2）当物块受F2作用时，由牛顿第二定律有：
加速度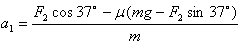
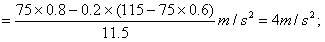
撤去F2后：μmg=ma2，a2=μg=2 m/s2
若要求外力作用时间最短，且到达B点，则到B点时速度为零。设F2最短作用时间为tmin
撤去F2时，物块速度为v'=a1tmin
则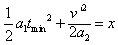
，代入数据解得tmin=2 s