l的方程为x=4或3x-4y+20=0.

当l的斜率存在时,由于直线l过点A(4,8),

可设l的方程为y-8=k(x-4),

即kx-y+4(2-k)=0,

又点B(1,2)到l的距离为3,

则,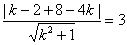

解方程得.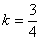

故所求直线的方程为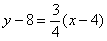

即3x-4y+20=0.

当l的斜率不存在时,过A(4,8)的直线方程为x=4,B(1,2)到它的距离也为3,

所以x=4也为所求.

综合知,l的方程为x=4或3x-4y+20=0.