问题
计算题
在2008年北京残奥会开幕式上,运动员手拉绳索向上攀登,最终点燃了主火炬,体现了残疾运动员坚韧不拔的意志和自强不息的精神。为了探求上升过程中运动员与绳索和吊椅间的作用,可将过程简化一根不可伸缩的轻绳跨过轻质的定滑轮,一端挂一吊椅,另一端被坐在吊椅上的运动员拉住,如图所示。设运动员的质量为65 kg,吊椅的质量为15 kg,不计定滑轮与绳子间的摩擦,重力加速度取g=10 m/s2。当运动员与吊椅一起正以速度a=1 m/s2上升时,试求:
(1)运动员竖直向下拉绳的力;
(2)运动员对吊椅的压力。
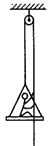
答案
解法一:(1)设运动员和吊椅的质量分别为M和m,绳拉运动员的力为F,以运动员和吊椅整体为研究对象,受到重力的大小为(M+m)g,向上的拉力为2F,根据牛顿第二定律
2F-(M+m)g=(M+m)a
F=440 N
根据牛顿第三定律,运动员拉绳的力大小为440 N,方向竖直向下
(2)以运动员为研究对象,运动员受到三个力的作用,重力大小Mg,绳的拉力F,吊椅对运动员的支持力FN。根据牛顿第二定律
F+FN-Mg=Ma
FN=275 N
根据牛顿第三定律,运动员对吊椅压力大小为275 N,方向竖直向下
解法二:设运动员和吊椅的质量分别为M和m,运动员竖直向下拉绳的力大小为F,对吊椅的压力大小为FN
根据牛顿第三定律,绳对运动员的拉力大小为F,吊椅对运动员的支持力大小为FN,分别以运动员和吊椅为研究对象,根据牛顿第二定律
F+FN-Mg=Ma ①
F-FN-mg=ma ②
由①②得F=440 N,FN=275 N(竖直向下)
