如图所示，一对平行金属板竖直固定在置于光滑水平面上的光滑绝缘

问题问答题

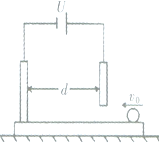
如图所示，一对平行金属板竖直固定在置于光滑水平面上的光滑绝缘板上，它们的总质量为M=0.8kg，金属板间距离为d=0.1m，金属板间加一电压为U=1.0×10⁶V的电源，一个质量为m=0.2kg，带电量为q=-2.0×10^-6 C的小球，以一定的初速度从右板底部小孔沿绝缘板射入两金属板之间，小球恰好不与左端金属板相碰，假设小球带电量始终保持不变，求：

（1）小球在两金属板之间运动时的加速度a；

（2）小球射入的初速度v₀的大小；

（3）从小球进入板间至小球刚要到达左侧金属板时，绝缘板向左滑行的距离s．

答案

（1）金属板间的场强E=

由牛顿第二定律得

小球的加速度a=

=100m/s²，方向水平向右．

（2）小球在两金属板之间运动时，系统动量守恒．设小球恰好不与左端金属板相碰时，系统的速度为v，由动量守恒定律得

mv₀=（M+m）v

又由能量守恒得

qU=

(M+m)v2

联立解得 v₀=5m/s

（3）以金属板为研究对象，根据动能定理得

qEs=

Mv2

代入解得 s=0.02m．

答：（1）小球在两金属板之间运动时的加速度a大小是100m/s²，方向水平向右；

（2）小球射入的初速度v₀的大小是5m/s；

（3）从小球进入板间至小球刚要到达左侧金属板时，绝缘板向左滑行的距离s是0.02m．