问题
计算题
如图所示，传送带与水平面的夹角为θ＝37°，以4m/s的速度向上运行，在传送带的底端A处无初速度地放一个质量为0.5kg的物体，它与传送带间动摩擦因数μ＝0.8，AB间（B为顶端）长度为25m。试回答下列问题：
（1）说明物体的运动性质。（相对地球）
（2）物体从A到B的时间为多少？（g＝10m/s2）
答案
解：（1）由题设条件知tan37°＝0.75，μ＝0.8，所以有tan37°<μ，这说明物体在斜面（传送带）上能处于静止状态，物体开始无初速度放在传送带上，起初阶段：对物体受力分析如图所示。
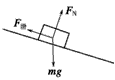
根据牛顿第二定律可知：F滑－mgsin37°＝ma，F滑＝μFN，FN＝mgcos37°
求解得a＝g（μcos37°－sin37°）＝0.4m/s2
设物体在传送带上做匀加速直线运动时间t1及位移x1，因v0＝0，a＝0.4m/s2，vt＝4m/s
根据匀变速直线运动规律得：vt＝at1，x1＝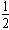
at12
代入数据得：t1＝10s，x1＝20m<25m
说明物体将继续跟随传送带一起向上匀速运动
物体在第二阶段匀速运动时间t2＝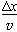
＝
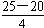s＝1.25s
所以物体运动性质为：物体起初由静止起以a＝0.4m/s2做匀加速直线运动，达到传送带速度后，便以传送带速度做匀速运动。
（2）物体运动总时间t总＝t1＋t2＝11.25s