问题
问答题
如图，直三棱柱ABC—A1B1C1中，AB⊥AC，D、E分别为AA1、B1C的中点，DE⊥平面BCC1．
(1)证明：AB=AC；
(2)设二面角A—BD—C为60°，求B1C与平面BCD所成的角的大小．
答案
参考答案：
解法一：(1)取BC中点F，连接EF，则
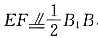，从而
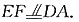
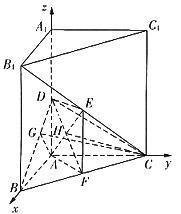
连接AF，则ADEF为平行四边形，从而AF∥DE，又DE⊥平面BCC1，故AF⊥平面BCC1，从而AF⊥BC，即AF为BC的垂直平分线，所以AB=AC.
(2)作AG⊥BD，垂足为G，连接CG，由三垂线定理知CG⊥BD，故∠AGC为二面角A—BD—C的平面角．由题设知，∠AGC=60°．
设AC=2，则
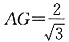，又AB=2，
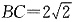，故
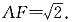
由AB·AD=AG·BD得
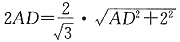，解得
，
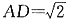故AD=AF，又AD⊥AF，所以四边形ADEF为正方形．
因为BC⊥AF，BC⊥AD，AF∩AD=A，故BC⊥平面DEF，因此平面BCD⊥平面DEF．
连接AE、DF，设AE∩DF=H，则EH⊥DF，EH⊥平面BCD，
连接CH，则∠ECH为B1C与平面BCD所成的角，
因ADEF为正方形，
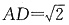，故EH=1，又
，
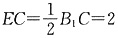所以∠ECH=30°，即B1C与平面BCD所成的角为30°．
解法二：(1)以A为坐标原点，射线AB为x轴的正半轴，建立如图所示的直角坐标系A—xyz.
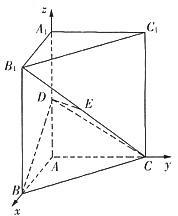
设B(1，0，0)，c(0，b，0)，D(0，0，c)，则B1(1，0，2c)，E(
，
).
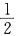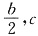于是
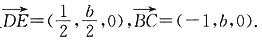由DE⊥平面BCC1知DE⊥BC，
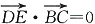，求得b=1，所以AB=AC.
(2)设平面BCD的法向量
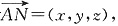则
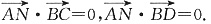又
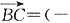1，1，0)，BD=(-1，0，c)，故
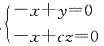
令x=1，则y=1，
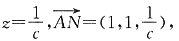
又平面ABD的法向量
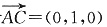
由二面角A—BD—C为60°知，
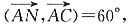
故
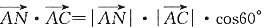，求得
.
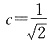于是
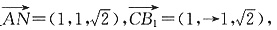
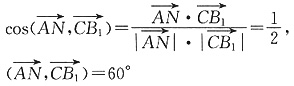
所以B1C与平面BCD所成的角为30°．