问题
填空题
| 在平面直角坐标系中,设点P(X,Y)定义[OP]=|x|+|y|,其中O为坐标原点,对于以下结论:①符合[OP]=1的点P的轨迹围成的图形的面积为2; ②设P为直线
③设P为直线y=kx+b(k,b∈R)上的任意一点,则“使[OP]最小的点P有无数个”的必要不充分条件是“k=±1”;其中正确的结论有______(填上你认为正确的所有结论的序号) |
答案
①由[OP]=1,根据新定义得:|x|+|y|=1,
可化为:
,y=-x+1(1≥x≥0) y=-x-1(-1≤x≤0) y=x+1(-1≤x≤0) y=x-1(1≥x≥0)
画出图象如图所示:
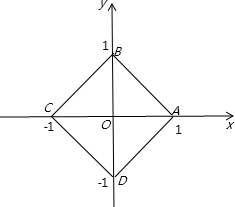
根据图形得到:四边形ABCD为边长是
的正方形,所以面积等于2,本选项正确;2
②当P(
,0)时,[OP]=|x|+|y|=2 5 5
<1,所以[OP]的最小值不为1,本选项错误;2 5 5
③因为|x|+|y|≥|x+y|=|(k+1)x+b|,当k=-1时,|x|+|y|≥|b|,满足题意;
而|x|+|y|≥|x-y|=|(k-1)x-b|,当k=1时,|x|+|y|≥|b|,满足题意,
所以“使[OP]最小的点P有无数个”的充要条件是“k=±1”,本选项错误.
则正确的结论有:①.
故答案为:①
