（10分）如图所示，在以坐标原点O为圆心、半径为R的半圆形区域内，有相互垂直的匀强电场和匀强磁场，磁感应强度为B，磁场方向垂直于xOy平面向里。一带正电的粒子（不计重力）从O点沿y轴正方向以某一速度射入，带电粒子恰好做匀速直线运动，经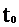
时间从p点射出。
（1）求电场强度的大小和方向。
（2）若仅撤去磁场，带电粒子仍从O点以相同的速度射入，经
时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
（3）若仅撤去电场，带电粒子仍从O点射入，且速度为原来的4倍，求粒子在磁场中运动的时间。
（1）
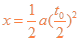，沿x轴正方向 （2）
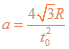（3）
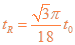
（1）设带电粒子的质量为m，电荷量为q，初速度为v，电场强度为E。可判断出粒子受到的洛伦磁力沿x轴负方向，于是可知电场强度沿x轴正方向
且有 qE=qvB ①
又 R=vt0 ②
则 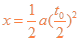③
（2）仅有电场时，带电粒子在匀强电场中作类平抛运动
在y方向位移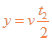 
④
由 ②④式得 
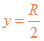⑤
设在水平方向位移为x，因射出位置在半圆形区域边界上，于是
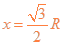
又有 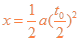⑥
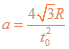得 ⑦
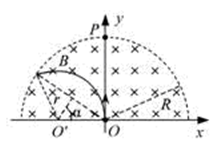
（3）仅有磁场时，入射速度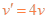
，带电粒子在匀强磁场中作匀速圆周运动，设轨道半径为r，由牛顿第二定律有
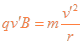⑧
又 qE=ma ⑨
由⑦⑧⑨式得 
⑩
由几何关系 
11
即 
12
带电粒子在磁场中运动周期
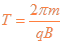
则带电粒子在磁场中运动时间
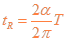
所以 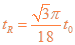13
