问题
填空题
直线ax+by-2=0,若适合3a-4b=1,则必过定点__________;若适合3a+2b=k(k≠0),则必过定点__________.
答案
(6,-8) 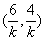
由3a-4b=1,解出b,代入ax+by-2=0,
消去b得a(4x+3y)=y+8.
∴过定点(6,-8).
同理,由3a+2b=k,解出b,代入ax+by-2=0,消去b得a(2x-3y)=4-yk,
∴过定点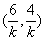 .
.
直线ax+by-2=0,若适合3a-4b=1,则必过定点__________;若适合3a+2b=k(k≠0),则必过定点__________.
(6,-8) 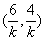
由3a-4b=1,解出b,代入ax+by-2=0,
消去b得a(4x+3y)=y+8.
∴过定点(6,-8).
同理,由3a+2b=k,解出b,代入ax+by-2=0,消去b得a(2x-3y)=4-yk,
∴过定点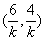 .
.