问题
解答题
求经过P(1，2)点和两条直线l1:x+y+1=0和l2:5x-3y+10=0的交点的直线方程.
答案
交点的直线方程11x-21y+31=0
经过l1和l1的交点的直线系方程为x+y+1+λ(5x-3y+10)=0.
∵点P(1，2)在所求的直线上，故1+2+1+λ(5×1-3×2+10)=0.
解得λ=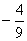
,将其代入直线系方程，得x+y+1-
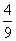(5x-3y+10)=0.
即11x-21y+31=0为所求.