问题
解答题
求证不论m取什么实数，直线(2m-1)x＋(m＋3)y-(m-11)=0都经过一个定点，并求出这个定点.
答案
定点为(2，-3).
令m=0，得x-3y-11=0；
令m=1，得x+4y+10=0.
解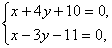
得两条直线的交点为(2，-3)，将点(2，-3)代入直线方程得(2m-1)×2+(m+3)×(-3)-(m-11)=4m-2-3m-9-m-11=0.
这说明不论m取什么实数，直线(2m-1)x+(m+3)y-(m-11)=0都经过一个定点，
这个定点为(2，-3).