问题
计算题
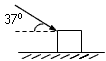
如图所示，一个放置在水平台面上的木块，其质量为2kg，受到一个斜向下的、与水平方向成37°角的推力F=10N的作用，使木块从静止开始运动，4s后撤去推力，若木块与水平面间的动摩擦因数为0.1。求：
（1）撤去推力F时木块的速度为多大？
（2）撤去推力F到停止运动过程中木块的加速度为多大？
（3）木块在水平面上运动的总位移为多少？
答案
解：（1）如图所示，撤去力F之前，由牛顿第二定律得：
水平方向：Fcos37°－f=ma ①
竖直方向：N－mg－Fsin37°=0 ②
又有：f=μN ③
由①②③得：a1=2.7m/s2 ④
由运动学公式：vt=v0+at
得，撤去力F时物块速度v=10.8m/s ⑤
（2）撤去力F后，由牛顿第二定律F=ma
得物块加速度a2=
=μg ⑥
解得a2=1m/s2 ⑦
（3）由运动学公式：
及④式得
撤去力F时物块位移s1=21.6m ⑧
由位移公式s=
及⑥式
得撤去力F后物块位移s2=58.32m ⑨
故物块在水平面上的总位移s=s1+s2=79.92m ⑩