问题
问答题
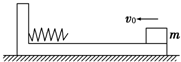
如图,质量为M的长木板静止在光滑水平地面上,在木板右端有质量为m的小物块,现给物块一个水平向左的初速度v0,物块向左滑行并与固定在木板左端的轻弹簧相碰,碰后返回并恰好停在长木板右端,求:
(1)弹簧弹性势能的最大值
(2)物块在木板上滑行过程中摩擦力做的总功.
答案
(1)设物块运动方向为正方向,弹簧压缩最大时,两者最终共同速度为v由动量守恒定律得:
(M+m)v=mvo
v=
vom M+m
由于物块最终停在木板最右端,故最终两者共同速度为v,由能量守恒得,整个过程放出的总热:
Q=
mvo2-1 2
(m+M)v2=1 2
vo2mM 2(m+M)
所以,弹簧压缩到最大时具有的弹性势能:
Ep=
=Q 2 mM 4(m+M)
(2)物块在木板上滑行过程中摩擦力做的总功数值上等于放出的热量,故:
Wf=Q=M mv 20 2(m+M)
答:(1)弹簧弹性势能的最大值为mM 4(m+M)
(2)摩擦力做的总功为M mv 20 2(m+M)
