如图所示,质量M=1.0kg的长木板静止在光滑水平面上,在长木板的右端放一质量m=1.0kg的小滑块(可视为质点),小滑块与长木板之间的动摩擦因数μ=0.20。现用水平恒力F=6.0N向右拉长木板,使小滑块与长木板发生相对滑动,经过t=1.0s撤去力F。小滑块在运动过程中始终没有从长木板上掉下。求:
(1)撤去力F时小滑块和长木板的速度各是多大?
(2)小滑块相对长木板静止时,小滑块相对地面运动的总位移。

解:(1)对长木板施加恒力F的时间内,小滑块与长木板间相对滑动,小滑块和长木板在水平方向的受力情况如图所示
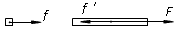
小滑块所受摩擦力f=μmg
设小滑块的加速度为a1,根据牛顿第二定律f=ma1
解得a1=2.0 m/s2
长木板受的摩擦力f ′=f=μmg
设长木板的加速度为a2,根据牛顿第二定律F-f ′=Ma2
解得a2= 4.0 m/s2
经过时间t=1.0 s,小滑块的速度v1=a1t=2.0 m/s
长木板的速度v2=a2t=4.0 m/s
(2)撤去力F后的一段时间内,小滑块的速度小于长木板的速度,小滑块仍以加速度a1做匀加速直线运动,长木板做匀减速直线运动。设长木板运动的加速度为a3,此时长木板水平方向受力情况如图所示
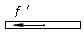
根据牛顿第二定律f ′=Ma3
解得a3=2.0 m/s2
设再经过时间t1后,小滑块与长木板的速度相等,此时小滑块相对长木板静止
即v1+a1t1=v2-a3t1
解得t1=0.50 s
如图所示,在对长木板施加力F的时间内,小滑块相对地面运动的位移是s1,从撤去F到二者速度相等的过程,小滑块相对地面的位移是s2
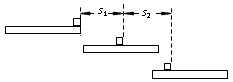
所以小滑块相对长木板静止时,小滑块相对地面运动的总位移为
s块=s1+s2=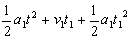 =2.25 m
=2.25 m
